
This page describes different ways in which physical systems can be represented mathematically. Generally system equations are derived as a set of differential equations. For example consider the system shown below (along with free body diagrams and system differential equations).
System:

Free Body Diagrams:
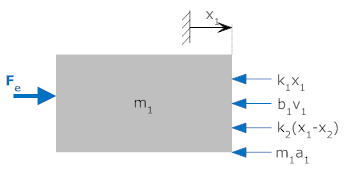
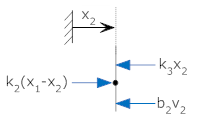
| Equations: | Free Body 1 (at x1) | Free Body 2 (at x2) | |
 |
 |
||
 |
 |
||
 |
 |
This representation completely represents the system, but is cumbersome to use. It requires two equations with multiple symbols and subscripts. It doesn't generalize well to a wide variety of systems. In this document we first review the representation of systems with differential equations, then we develop several systems that are generally easier to work with.
Keep in mind that this document describes the various forms (e.g., transfer function, state space...) but does not discuss their solution. That discussion is elsewhere, and separated by discipline:
This document introduces several system representations (transfer function, state space, ...) for the same system. The prefered representation depends on the task at hand, but in the end they must all represent the same system. Procedures for transforming from one representation to another are given in the document accessed by the "Transformations" tab at the top of this page.