The previous page showed that a time domain signal can be represented as a sum of sinusoidal signals (i.e., the frequency domain), but the method for determining the phase and magnitude of the sinusoids was not discussed. This page will describe how to determine the frequency domain representation of the signal. For now we will consider only periodic signals, though the concept of the frequency domain can be extended to signals that are not periodic (using what is called the Fourier Transform). The next page will give several examples.
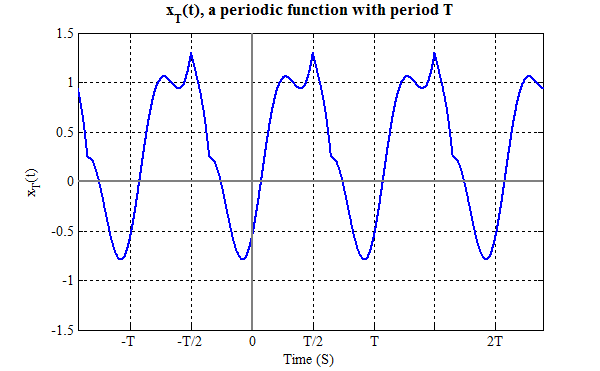
Consider a periodic signal xT(t) with period T (we will write periodic signals with a subscript corresponding to the period). Since the period is T, we take the fundamental frequency to be ω0=2π/T. We can represent any such function (with some very minor restrictions) using Fourier Series.

In the early 1800's Joseph Fourier determined that such a function can be represented as a series of sines and cosines. In other words he showed that a function such as the one above can be represented as a sum of sines and cosines of different frequencies, called a Fourier Series. There are two common forms of the Fourier Series, "Trigonometric" and "Exponential." These are discussed below, followed by a demonstration that the two forms are equivalent. For easy reference the two forms are stated here, their derivation follows.
$$The Fourier Series is more easily understood if we first restrict ourselves to functions that are either even or odd. We will then generalize to any function.
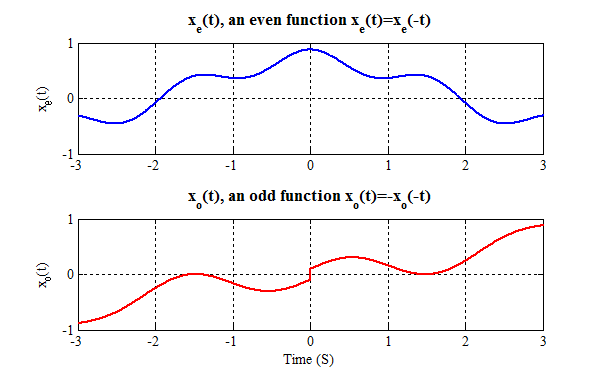
The following derivations require some knowledge of even and odd functions, so a brief review is presented. An even function, xe(t), is symmetric about t=0, so xe(t)=xe(-t). An odd function, xo(t), is antisymmetric about t=0, so xo(t)=-xo(-t) (note: this implies that xo(0)=0). Examples are shown below.
Other important facts about even and odd functions:
An even function, xe(t), can be represented as a sum of cosines of various frequencies via the equation:
$$ x_e (t) = \sum\limits_{n = 0}^\infty {a_n \cos \left( {n\omega _0 t} \right)} $$
Since cos(nω0t)=1 when n=0 the series is more commonly written as
$$ x_e (t) = a_0 + \sum\limits_{n = 1}^\infty {a_n \cos \left( {n\omega _0 t} \right)} $$
This is called the "synthesis" equation because it shows how we create, or synthesize, the function xe(t) by adding up cosines.
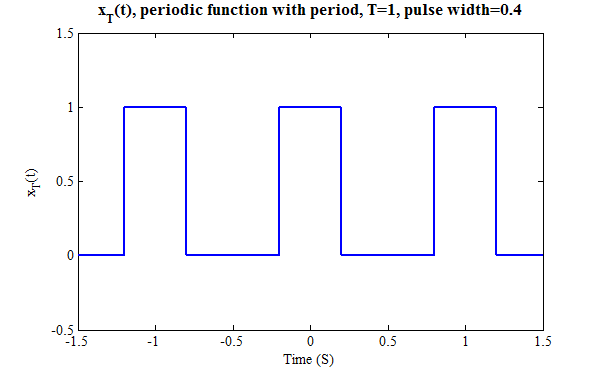
An example will demonstrate exactly how the summation describing the synthesis process works. Consider the following function, xT and its corresponding values for an. This function has T=1 so ω0=2·π/T=2·π. Note: we have not determined how the an are calculated; that derivation follows, that calculation comes later.
|
 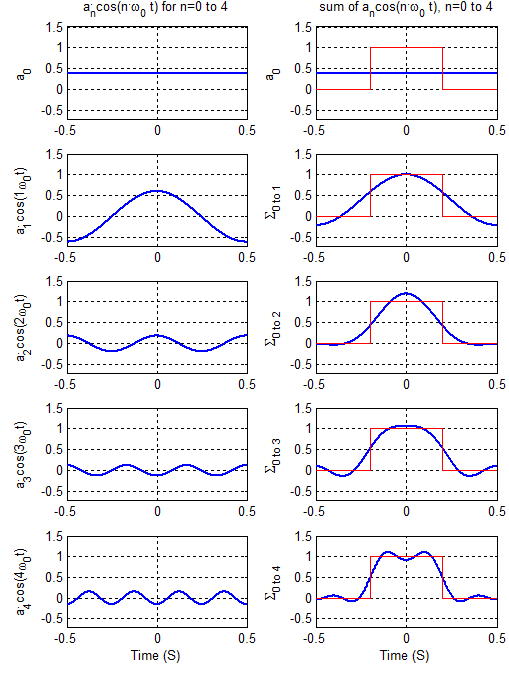 |
The right column shows the sum $$ a_0 + \sum\limits_{n = 1}^N {a_n \cos \left( {n\omega _0 t} \right)} $$ for n=0 to 4.
The example above shows how the harmonics add to approximate the original question, but begs the question of how to find the magnitudes of the an. Start with the synthesis equation of the Fourier Series for an even function xe(t) (note, in this equation, that n≥0).
$$ x_e (t) = \sum\limits_{n = 0}^\infty {a_n \cos ( n\omega _0 t)} $$Now, without justification we multiply both sides by $\cos(m\omega_0t)$
$$then integrate over one period (note: the exact interval is unimportant, but we will generally use -T/2 to T/2 or 0 to T, depending on which is more convenient).
$$ \int\limits_T {x_e (t)\cos \left( {m\omega _0 t} \right)dt} = \int\limits_T {\sum\limits_{n = 0}^\infty {a_n \cos \left( {n\omega _0 t} \right)} \cos \left( {m\omega _0 t} \right)dt} $$Now switch the order of summation and integration on the right hand side, followed by application of the trig identity cos(a)cos(b)=½(cos(a+b)+cos(a-b))
$$ \begin{align}Consider only the cases when m>0, then the function cos((m+n)ω0t) has exactly (m+n) complete oscillations in the interval of integration, T. When we integrate this function, the result is zero (because we are integrating over an an integer (greater than or equal to one) number of oscillations). This simplifies our result to
$$ \begin{align}Since cosine is an even function cos((m-n)ω0t)=cos((n-m)ω0t) is time varying and has exactly |m-n| complete oscillations in the interval of integration, except when m=n in which case cos((m-n)ω0 = cos(0) = 1 so
Now look at the summation again
$$ \int\limits_T {x_e (t)\cos \left( {m\omega _0 t} \right)dt} = {1 \over 2}\sum\limits_{n = 0}^\infty {a_n \int\limits_T {\cos \left( {\left( {m - n} \right)\omega _0 t} \right)dt} } $$As n goes from 0 to ∞ every term in the summation except when m=n will be zero. So the only term that contributes to the summation is m=n, when the integral equals T. So the entire summation reduces to
$$We switched m to n in the last line since m is just a dummy variable. We now have an expression for an, which was our goal.
In the text above, the equating of the two terms
$$is often puzzling. To explain it, take m=2 and expand the summation
$$\begin{align}In the last line we used the fact that cos(0)=1 and cos(-x)=cos(x). All of the integrals but the third one will go to zero because the integration is over an integer number of oscillations (as will all of the omitted terms). The third integral becomes a2T, as was expected.
(you may skip this if you would like to - it is not necessary to proceed).
In the discussion above we use the fact that
$$This is called the orthogonality function of the cosine. It is similar to orthogonality of vectors. Consider two vectors and their dot product.
$$We say the vectors x and y are orthogonal if their dot product (the sum the elementwise products of the vectors' elements) is zero. If we switch integral for sum (since the function is a continuous function of time) we say functions are orthogonal if the integral of the product of the two functions is zero.
The derivation of the Fourier series coefficients is not complete because, as part of our proof, we didn't consider the case when m=0. (Note: we didn't consider this case before because we used the argument that cos((m+n)ω0t) has exactly (m+n) complete oscillations in the interval of integration, T). For the special case m=0
$$This leads to the result stated above, that a0 is the average value of the function
$$ a_0 = \frac{1} {T}\int\limits_T {x_e (t)dt} = {\text{average of x}}_e \left( t \right) $$An odd function can be represented by a Fourier Sine series (to represent even functions we used cosines (an even function), so it is not surprising that we use sinusoids.
$$Note that there is no b0 term since the average value of an odd function over one period is always zero.
The coefficients bn can be determined from the equation
$$ The derivation closely follows that for the an coefficients.
Any function can be composed of an even and an odd part. Given a function x(t), we can create even and odd functions
$$Clearly, xo(t)=-xo(-t) and xe(t)=xe(-t), and when added together they create the original function. x(t)=xo(t)+xe(t). We can use a Fourier cosine series to find the an associated with xe(t) and a Fourier sine series to find the bn associated with xo(t).
Given a periodic function xT, we can represent it by the Fourier series synthesis equations
$$ x_T \left( t \right) = a_0 + \sum\limits_{n = 1}^\infty {\left( {a_n \cos \left( {n\omega _0 t} \right) + b_n \sin \left( {n\omega _0 t} \right)} \right)} $$We determine the coefficients an and bn are determined by the Fourier series analysis equations
$$A more compact representation of the Fourier Series uses complex exponentials. In this case we end up with the following synthesis and analysis equations:
$$The derivation is similar to that for the Fourier cosine series given above. Note that this form is quite a bit more compact than that of the trigonometric series; that is one of its primary appeals. Other advantages include: a single analysis equation (versus three equations for the trigonometric form), notation is similar to that of the Fourier Transform (to be discussed later), it is often easier to mathematically manipulate exponentials rather sines and cosines. A principle advantage of the trigonometric form is that it is easier to visualize sines and cosines (in part because the cn are complex number,, and the series can be easily used if the original xT is either purely even or odd.
If the trigonometric
$$ x_T \left( t \right) = a_0 + \sum\limits_{n = 1}^\infty {\left( {a_n \cos \left( {n\omega _0 t} \right) + b_n \sin \left( {n\omega _0 t} \right)} \right)} $$and exponential forms
$$x_T \left( t \right) = \sum\limits_{n = - \infty }^{ + \infty } {c_n e^{jn\omega _0 t} }$$of the Fourier series are equivalent, then
$$a_0 + \sum\limits_{n = 1}^\infty {\left( {a_n \cos \left( {n\omega _0 t} \right) + b_n \sin \left( {n\omega _0 t} \right)} \right)} = \sum\limits_{n = - \infty }^{ + \infty } {c_n e^{jn\omega _0 t} }$$This begs the question of how the cn terms are related to the an and bn terms. In the following discussion it is assumed that xT is real so an and bn are real. To start consider only the constant terms
$$a_0=c_0$$.So c0 is also the average of the function xT. Likewise if we consider only those parts of the signal that oscillate once in a period of T seconds we get
$$ a_1 \cos (\omega _0 t) + b_1 \sin (\omega _0 t) = c_{ - 1} e^{ - j\omega _0 t} + c_1 e^{ + j\omega _0 t} $$and for two oscillations in T seconds we get
$$ a_2 \cos (2\omega _0 t) + b_2 \sin (2\omega _0 t) = c_{ - 2} e^{ - j2\omega _0 t} + c_2 e^{ + j2\omega _0 t} $$and in general
$$ a_n \cos (n\omega _0 t) + b_n \sin (n\omega _0 t) = c_{ - n} e^{ - jn\omega _0 t} + c_n e^{ + jn\omega _0 t} $$Obviously the left side of this equation is real, so the right side must also be real. Since e-jnω₀t is the complex conjugate of e+jnω₀t so c-n must be the complex conjugate of cn so the imaginary parts cancel when added. If we write cn = cn,r + j·cn,i (sum of real and imaginary parts), then c-n = c*n = cn,r - j·cn,i. So (using Euler's identities),
$$so, equating the magnitude of cosine and sine terms (with n≠0)
$$ \displaylines{ a_n = 2c_{n,r} \cr b_n = -2c_{n,i} \cr} $$or
$$c_n=\frac{a_n}2-j\frac{b_n}2, \ n \ne 0, \quad with \ c_{-n}=c_n^*$$The trigonometric
$$ x_T \left( t \right) = a_0 + \sum\limits_{n = 1}^\infty {\left( {a_n \cos \left( {n\omega _0 t} \right) + b_n \sin \left( {n\omega _0 t} \right)} \right)} $$and exponential
$$x_T \left( t \right) = \sum\limits_{n = - \infty }^{ + \infty } {c_n e^{jn\omega _0 t} }$$forms of the Fourier Series are equivalent with
$$a_0 = c_0$$and for n≠0
$$ \eqalign{ c_n &= c_{n,r} + j c_{n,i}\cror
$$ c_n=\frac{a_n}2-j\frac{b_n}2 ,\quad with \ c_{-n}=c_n^*$$As stated earlier, there are certain limitations inherent in the use of the Fourier Series. These are almost never of interest in engineering applications. In particular, the Fourier series converges
At a discontinuity there is an overshoot (Gibb's phenomenon - about 9% for a square wave). However this discontinuity becomes vanishingly narrow (and it's area, and energy, are zero), and therefore irrelevant as we sum up more terms of the series.
After you have studied Fourier Transforms, you will learn that there is an easier way to find Fourier Series coefficients for a wide variety of functions that does not require any integration.