
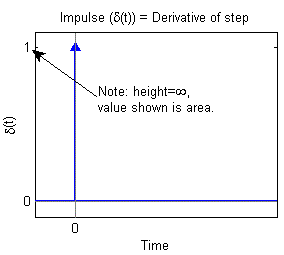
One of the more useful functions in the study of linear systems is the "unit impulse function." An ideal impulse function is a function that is zero everywhere but at the origin, where it is infinitely high. However, the area of the impulse is finite. This is, at first hard to visualize but we can do so by using the graphs shown below.

Consider first the ramp function shown in the upper left. It is zero
for t<0 and one for t>T, and goes linearly from 0 to 1 as time goes from 0 to T.
If we let T→0, we get a unit step function,
γ(t) (upper right).
If we take the derivative of our ramp function (lower left), we get a
rectangular pulse with height 1/T (the slope of the line) and width T.
This rectangular pulse has area (height·width) of one. If we take
the limit as T→0, we get a pulse of infinite height, zero width, but still
with an area of one; this is the unit impulse and we represent it by
δ(t). Since we can't show the height of the impulse on our graph,
we use the vertical axis to show the area. The unit impulse has area=1, so
that is the shown height.
Note: this derivation of an impulse function is not unique. The
important result is that the function has zero width and an area of one.
The relationship between step function and impulse function is even more obvious in the Laplace Domain (Note: if you haven't studied Laplace Transforms, you may skip this paragraph). The definitions for both are given below.
| Step Function | Impulse Function | |
| \[\gamma (t)\overset L \longleftrightarrow \Gamma (s) = \frac{1}{s}\] | \[\delta (t)\overset L \longleftrightarrow \Delta (s) = 1\] |
Clearly from these definitions we have Δ(s)=s·Γ(s). Since multiplication by "s" in the Laplace Domain is equivalent to differentiation in time this tells us that the unit impulse function is simply the derivative of the unit step function.
The unit impulse function has zero width, infinite height and an integral (area) of one. We plot it as an arrow with the height of the arrow showing the area of the impulse.
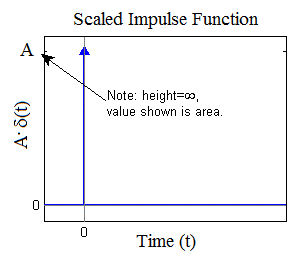
To show a scaled input on a graph, its area is shown on the vertical axis. In the diagram below the area of the impulse function is "A." For a scaled impulse (i.e., A·δ(t)), the multiplier in front of the impulse is the area.
Note, there are other, equally valid, definitions of an impulse. The only important result is that the function has width approaching zero, height approaching infinity and an area of one. For example, consider a Gaussian curve.
\[f\left( x \right) = \frac{1}{{\sqrt {2\pi {\sigma ^2}} }}{e^{ - \frac{{{x^2}}}{{2{\sigma ^2}}}}}\]It is well known that the area under this graph is always one one (ref). The graph below shows the function for several values of σ.

Clearly as σ→0, f(0)→∞, and the width→0, but the area under the curve remains one. This definition of the impulse is often used in statistics.
The integral of the impulse is one. So if we consider the integral (with b>a)
\[\int\limits_a^b {\delta (t)dt} = \left\{ {\begin{array}{*{20}{c}} {1,\quad a < 0 < b}\\ {0,\quad otherwise} \end{array}} \right.\]In other words, if the integral includes the origin (where the impulse lies), the integral is one. If it doesn't include the origin, the integral is zero.
Likewise, and by similar reasoning, if the impulse is not at the origin (and b>a)
\[\int\limits_a^b {\delta (t - \lambda )dt} = \left\{ {\begin{array}{*{20}{c}} {1,\quad a < \lambda < b}\\ {0,\quad otherwise} \end{array}} \right.\]Let us now evaluate the integral of a function multiplied by an impulse at the origin.
\[\int\limits_{ - \infty }^{ + \infty } {\delta (t) \cdot f(t)dt} \]We can simplify this integral by noting that because the impulse is zero everywhere except when t=0 we can replace δ(t)·f(t) by δ(t)·f(0).
\[\int\limits_{ - \infty }^{ + \infty } {\delta (t) \cdot f(t)dt} = \int\limits_{ - \infty }^{ + \infty } {\delta (t) \cdot f(0)dt} \]This is a powerful statement; it means we can replace the product of two functions (), which is typically difficult integrate, and replace it by the product of a function and a constant () which is easy to integrate. We continue the deivation by pulling f(0) out of the integral (because it is a constant). So
\[ {\eqalign {\int\limits_{ - \infty }^{ + \infty } {\delta (t) \cdot f(t)dt} &= \int\limits_{ - \infty }^{ + \infty } {\delta (t) \cdot f(0)dt} \\ &= f(0) \cdot \int\limits_{ - \infty }^{ + \infty } {\delta (t)dt} \\ &= f(0)}} \]More generally, and by the same reasoning, we can write (with b>a)
\[\eqalign{ \int\limits_a^b {\delta (t) \cdot f(t)dt} &= \int\limits_a^b {\delta (t) \cdot f(0)dt} \\ &= f(0) \cdot \int\limits_a^b {\delta (t)dt} \\ &= \left\{ {\begin{array}{*{20}{c}} {f(0),\quad a < 0 < b}\\ {0,\quad otherwise} \end{array}} \right. }\]Likewise because δ(t-λ) is zero except at t=λ we can show (if b>a)
\[\int\limits_a^b {\delta (t - \lambda ) \cdot f(t)dt} = \left\{ {\begin{array}{*{20}{c}} {f(\lambda ),\quad a < \lambda < b}\\ {0,\quad otherwise} \end{array}} \right.\] This is called the "sifting" property because the impulse function δ(t-λ) sifts through the function f(t) and pulls out the value f(λ).If a<b, then
\[\int\limits_a^b {\delta (t - \lambda ) \cdot f(t)dt} = \left\{ {\begin{array}{*{20}{c}} {f(\lambda ),\quad a < \lambda < b}\\ {0,\quad otherwise} \end{array}} \right.\]This is called the "sifting" property because the impulse function d(t-λ) sifts through the function f(t) and pulls out the value f(λ).
Said another way, we replace the value of "t" in the function f(t) by the value of "t" that makes the argument of the impulse equal to 0 (in this case, t=λ).
Note: often the limits of integration are ±∞ so the result is simply f(λ).
Assume a<b, and evaluate the integral
\[\int\limits_a^b {\delta (t) \cdot f(t - \lambda )dt} \]
Solution:
We now that the
impulse is zero except at t=0 so
and
\[\eqalign{ \int\limits_a^b {\delta (t) \cdot f(t - \lambda )dt} &= \int\limits_a^b {\delta (t) \cdot f( - \lambda )dt} \\ &= f( - \lambda ) \cdot \int\limits_a^b {\delta (t)dt} \\ &= \left\{ {\begin{array}{*{20}{c}} {f( - \lambda ),\quad a < 0 < b}\\ {0,\quad otherwise} \end{array}} \right. }\]Again, we replace the value of "t" in the function that makes the argument of the impulse equal to 0 (in this case, t=0).
Another important property of the impulse is that convolution of a function with a shifted impulse (at a time t=T0 ) yields a shifted version of that function (also shifted by T0).
\[f(t) * \delta (t - {T_0}) = f(t - {T_0})\]We prove this by using the definition of convolution (first line, below). By the sifting property, we replace "λ" in the function by the value of "λ" that makes the argument of the impulse equal to zero (in this case λ=T0) and we get the desired result (the third line).
\[\eqalign{ f(t) * g(t) &= \int\limits_{ - \infty }^{ + \infty } {f(t - \lambda )g(\lambda )d\lambda } \\ f(t) * \delta (t - {T_0}) &= \int\limits_{ - \infty }^{ + \infty } {f(t - \lambda )\delta (\lambda - {T_0})d\lambda } \\ f(t) * \delta (t - {T_0}) &= f(t - {T_0}) }\]Convolution of a function with a shifted impulse yields a shifted version of that function.
\[f(t) * \delta (t - {T_0}) = f(t - {T_0})\]We can also do the proof using the alternate form of the impulse (recall that the convolution is commutative).
\[\eqalign{ f(t) * g(t) &= \int\limits_{ - \infty }^{ + \infty } {f(\lambda )g(t - \lambda )d\lambda } \\ f(t) * \delta (t - {T_0}) &= \int\limits_{ - \infty }^{ + \infty } {f(\lambda )\delta (t - \lambda - {T_0})d\lambda } \\ f(t) * \delta (t - {T_0}) &= f(t - {T_0}) \\ } \]In the second line the argument to the impulse is zero when λ=t-T0, so we replace λ in f(λ) by t-T0 to get the final result.
© Copyright 2005 to 2019 Erik Cheever This page may be freely used for educational purposes.
Erik Cheever Department of Engineering Swarthmore College